S-hull.org now offers GPL version of the C++ code for s-hull-pro and s-hull-pro-INTEGER as well as s-hull-3D (christened the Newton Apple Wrapper algorithm for 3D convex hulls AND Delaunay triangulations).
If you need a non GPL version please look at
commercial licensing.
If you like the code and would like to make a donation of 4.00 pounds Sterling that I WILL spend on beer then please use the buy it now button:). This also gives you a non GPL licnse to the C++ s-hull-pro and s-hull-pro-integer and s-hull-3D (NA_wrapper)code!
S-Hull Algorith Description.
A new O(nlog(n)) algorithm is presented for performing Delaunay triangulation of sets of 2D points.
The novel component of the algorithm is a radially propagating sweep-hull (sequentially created from
the radially sorted set of 2D points),
paired with a final triangle flipping step to give the Delaunay triangluation.
In empirical tests the algorithm runs in approximately half the time of q-hull for 2D Delaunay
triangulation on randomly generated point sets.
S-hull operates as follows:
For a set of unique points x_i in R2:
1: sellect a seed point x_0 from x_i.
2: sort according to |x_i - x_0|^2.
3: find the point x_j closest to x_0.
4: find the point x_k that creates the smallest circum-circle with x_0 and x_j
and record the center of the circum-circle C.
5: order point x_0, x_j, x_k to give a right handed system
thi is the initial seed convex hull.
6: resort the remaining points according to x_i - C|^2 to give points s_i.
7: sequentially add the points s_i to the porpagating 2D convex hull
that is seeded with the triangle formed from x_0, x_j, x_k .
as a new point is added the facets of the 2D-hull that are visible to it form new triangles.
8: a non-overlapping triangulation of the set of points is created.
(This is an extremely fast method for creating an non-overlapping triangualtion of a 2D point set).
9: adjacent pairs of triangles of this triangulation must be 'flipped' to create a Delaunay triangulation
from the initial non-overlapping triangulation.
The algorithm generates a Delaunay triangulation together with the 2D convex hull for set of points.
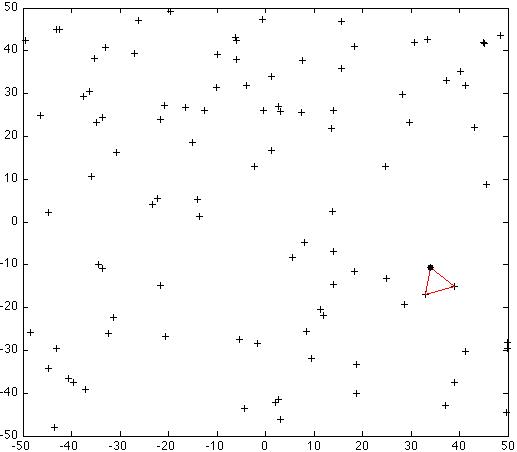
1: a randomly generated set of 100 points in R2 with the initial
triangular seed hull marked in red and the starting seed point in
black.
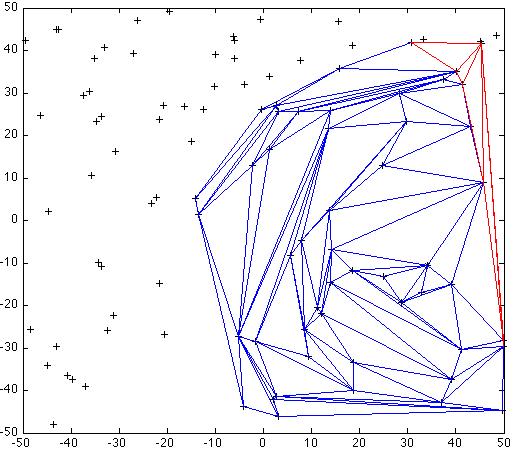
2: propagation of the sweep-hull, new triangles in red, existing triangles in blue.
 .
.
3: the delaunay triangulation generated by s-hull.
Table 1 gives empirical times for s-hull and q-hull for point sets that
range in size form 100 to 1,000,000. S-hull is empirically faster. The
test code was compiled and run on a MacBook Pro using gcc
i686-apple-darwin9-g++-4.0.1 .
| Algorithm |
100 pts |
1000 pts |
10,000 pts |
100,000 pts |
1,000,000 pts |
| Q-hull |
0.001263 |
0.01154 |
0.1095 |
1.961 |
24.32 seconds |
| S-hull |
0.000751 |
0.005682 |
0.0766 |
1.044 |
14.490 |
S-hull exists to further the art of Delaunay triangulation and associated distance transform based techniques.
Various delaunay triangulation resources include:
q-hull used by MatLab,
sweep-line: Steven Fortune's homepage,
NetLib ,
Jonathan Shewchuck's homepage .
Contributions
The code on s-hull.org is released under a contributor's beerware license (details in the Ts&Cs).
An implementations of s-hull have been contributed by Phil Atkin in C# and a Python binding by Christian Delfosse.
If you think s-hull if worth it and you meet Phil Atkin or Dr Sinclair or Chritian Delfosse in a pub or bar you
could by them a beer, alternatively you could email david@s-hull.org and arrange to make a donation
of 10 of your local currancy units to support s-hull.org.



 .
.